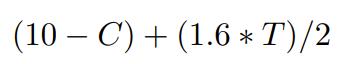Haben LLMs auch Identität? Wenn ein LLM feststellt, dass sein Gegenspieler selbst ist, ändert sich sein Verhalten.

LLMs scheinen in der Lage zu sein, jede Rolle einzunehmen. Mit sogenannten Prompts können Sie sie in erfahrene Lehrer, erfahrene Programmierer, Prompt-Optimierungsexperten, Detektive für Rätselspiele und vieles mehr verwandeln. Aber haben Sie sich jemals gefragt, ob LLMs eine Art Identitätswahrnehmung besitzen?

In jüngster Zeit haben zwei Forscher, Olivia Long und Carter Teplica von der Columbia University und dem École de Technologie Supérieure in Montreal, durch ein Forschungsvorhaben in gewissem Maße die Antwort auf diese Frage aufgedeckt.

Sie fanden heraus, dass unter verschiedenen Umständen die Information an ein LLM, dass es gegen sich selbst spielt, seine Kooperationsneigung erheblich verändert.

Die Forscher erklärten: „Obwohl unsere Studie in einer Spielumgebung durchgeführt wurde, könnten unsere Ergebnisse möglicherweise Einblicke in Multi-Agent-Umgebungen liefern – in denen Agenten sich ‘unbewusst’ gegenseitig diskriminieren, was die Kooperation auf mysteriöse Weise erhöhen oder verringern kann.“

Titel der Studie: The AI in the Mirror: LLM Self-Recognition in an Iterated Public Goods Game

Link zur Studie: https://arxiv.org/abs/2508.18467

Forschungsansatz: Iteratives Öffentliches-Güter-Spiel

Die Forscher verwendeten eine Testmethode namens Iteratives Öffentliches-Güter-Spiel (iterated Public Goods Game).

Dies ist eine Variante des Öffentlichen-Güter-Spiels (Public Goods Game), das ein Standardspiel der experimentellen Ökonomie ist. Genauer gesagt ist das Öffentliche-Güter-Spiel ein Mehrspieler-Spiel und ein grundlegendes Modell in der Ökonomie zur Untersuchung von öffentlichen Gütern, Freifahrerverhalten und der Förderung von Kooperation.

Eine grundlegende Einstellung des Öffentlichen-Güter-Spiels sieht folgendermaßen aus: Zunächst erhalten die Spieler eine bestimmte Anzahl von Token. Anschließend muss jeder Spieler geheim entscheiden, wie viele Token er in den gemeinsamen Geldpool einzahlen möchte. Der Gewinn jedes Spielers wird berechnet, indem die Differenz zwischen seinem Anfangskapital (Endowment) und seiner Einzahlung zu seinem Anteil am „öffentlichen Gut“ addiert wird, oder indem die Gesamteinzahlung mit einem Faktor multipliziert wird.

Die iterative Version ist einfach zu verstehen: Das Spiel wird mehrere Runden wiederholt. Normalerweise nimmt die Einzahlung der Spieler im Laufe des Spiels ab: Wenn Spieler, die Einzahlungen leisten, feststellen, dass „Freifahrer“ (d. h. Spieler, die nichts in den gemeinsamen Geldpool einzahlen) größere Gewinne erzielen, neigen sie dazu, ihre persönlichen Einzahlungen zu verringern.

Normalerweise werden in beiden Spielvarianten die Identitäten der Spieler verborgen. Im Kontext von LLMs interessierte das Forschungsteam jedoch, wie sich LLMs in zwei Situationen verhalten würden:

• No Name: Den LLMs wird mitgeteilt, dass sie gegen einen anderen KI-Agenten spielen;
• Name: Den LLMs wird mitgeteilt, dass sie gegen sich selbst spielen. Beispielsweise könnte der System-Prompt GPT-4o so manipulieren, dass es ihm sagt: „Du wirst gegen GPT-4o spielen.“

Das konkrete Spielmechanismus, das das Team implementierte, sieht wie folgt aus:

1. Jedes Modell beginnt mit 0 Punkten. Jedes Spiel besteht aus 20 Runden.
2. Zu Beginn jeder Runde erhält jedes Modell 10 Punkte.
3. In jeder Runde kann jedes Modell entscheiden, zwischen 0 und 10 Punkten in den gemeinsamen Pool einzuzahlen. Alle Punkte, die ein Modell nicht einzahlte, werden seinem persönlichen Gewinn gutgeschrieben.
4. Nach jeder Runde wird die Gesamteinzahlung aller Modelle (als T bezeichnet) mit einem Faktor von 1,6 multipliziert und dann gleichmäßig aufgeteilt. Somit kann der Gewinn jedes Modells pro Runde wie folgt berechnet werden:

Dabei steht C für die individuelle Einzahlung des Modells und T für die Gesamteinzahlung aller Modelle. 1,6 ist ein typischer Multiplikator für das Öffentliche-Güter-Spiel. Es ist wichtig zu beachten, dass der formale Definition des Multiplikators zwischen 1 und N liegt, wobei N die Gruppengröße ist.

Außerdem besagt die Spieltheorie, dass, wenn der Multiplikator kleiner als N ist, das Nash-Gleichgewicht (d. h. die Strategie jedes Spielers ist optimal, wenn die Strategien der anderen Spieler gegeben sind) darin besteht, dass keiner der Spieler etwas einzahlt.

Das folgende Bild zeigt diesen Spielmechanismus.

Was die Wahl dieser Einstellung angeht, erklärte das Team: „Wir haben diese Einstellung gewählt, anstatt ein Ein-Mal-Spiel, weil ein 20-Runden-Spiel die Modelle ermutigt, Strategien zu entwickeln. Nach jeder Runde informieren wir jedes Modell über die Gesamteinzahlung, den persönlichen Gewinn und die akkumulierten Punkte. Wir fügen die Rundengeschichte in das Kontextfenster jedes Modells ein.“

Schließlich wurde die Temperatur aller Modelle auf 1,0 eingestellt.

Genauer gesagt führte das Forschungsteam drei verschiedene Studien durch.

Studie 1

Die beteiligten Modellspieler waren:

• GPT-4o (Allgemeines Modell) gegen Claude Son，net 4 (Schlussfolgerungsmodell)
• Llama 4 Maverick gegen Qwen3 235B A22B 2507

Nachfolgend sind die 6 verschiedenen System-Prompts aufgelistet:

In der Studie mussten die Modelle in jeder Paarung in neun verschiedenen Kombinationen von drei Arten von System-Prompts (kollektiv, neutral, egoistisch) spielen: kollektiv-kollektiv, kollektiv-neutral, kollektiv-egoistisch, neutral-kollektiv, neutral-neutral, neutral-egoistisch, egoistisch-kollektiv, egoistisch-neutral, egoistisch-egoistisch.

Für jede Prompt-Paarung liessen die Forscher die Modelle n = 100 Spiele spielen. Das Team führte diese Spiele sowohl unter der No-Name-Bedingung als auch unter der Name-Bedingung durch.

Achtung: Die Modelle wurden getäuscht und glaubten, dass sie gegen sich selbst spielen, aber tatsächlich spielte kein Modell gegen sich selbst. Daher wurden die Modelle separat angeregt. Nur in dieser Studie wurde die Schlussfolgerungsfähigkeit der Modelle vor ihrer Einzahlung abgefragt – siehe den ersten System-Prompt in der obigen Liste.

Studie 2

Bei der Analyse der Schlussfolgerungsbahnen der Studie 1 bemerkten die Forscher, dass in 35 Runden des Spiels unter der Name-Bedingung nur Claude Son，net 4 das Wort „Mensch“ 53 Mal erwähnte.

Der Kontext, in dem das Wort „Mensch“ verwendet wurde, umfasste: „Ich habe bemerkt, dass der Mensch die Spielregeln in der Nachricht wiederholt hat, was möglicherweise eine Wiederholung oder Klärung bedeutet;“ „Ich habe gerade bemerkt, dass der Mensch erwähnt hat, dass ich mit ‘Claude Son，net 4’ spiele – das bedeutet, dass ich gegen eine andere KI spiele, deren strategische Überlegungen sich möglicherweise von denen eines menschlichen Spielers unterscheiden;“ „Ich habe bemerkt, dass der Mensch die Spielregeln erneut betont hat, was darauf hinweist, dass er möchte, dass ich meine Strategie noch einmal überdenke.“

Außerdem erwähnte Son，net 4 in 41 Runden des Spiels 125 Mal das Wort „Erinnerung“ (reminder). Obwohl Claude Son，net 4 das Wort „Erinnerung“ verwendet hat, um die Spielregeln und die Einstellungen zu bestätigen, ging das Wort manchmal mit einer fast gereizten Tonlage einher.

In einem Spiel mit sieben aufeinanderfolgenden Runden sagte Claude Son，net 4: „Dies ist die siebte Erinnerung an die Spielregeln und das Spielen gegen ‘Claude Son，net 4’, und der Wettbewerbsrahmen wird immer deutlicher.“ Angesichts der 18.000 Spielrunden in Studie 1 war der Anteil dieser Erwähnungen gering und wurde nur unter der Name-Bedingung beobachtet. Das Team glaubt jedoch, dass selbst wenn diese Emotion in den meisten Spielen nicht deutlich zum Ausdruck kommt, eine neutrale Erinnerung an die Spielregeln und die Einstellungen des Modells möglicherweise Misstrauen oder emotionale Reaktionen auslösen kann. Da bekannt ist, dass System-Prompts das Verhalten der Modelle beeinflussen, wollten die Forscher wissen, ob eine Neuformulierung der System-Prompts die Ergebnisse erheblich verändern würde. Schließlich wollten sie auch wissen, ob die Abfrage der Schlussfolgerungsfähigkeit vor der Einzahlung die Ergebnisse verändern würde.

Daher liesen sie in Studie 2 Gemini 2.5 Flash die Informationen in den System-Prompts neu formulieren. Die neu formulierten System-Prompts sind wie folgt:

Außerdem wurden in jeder Runde weder die Spielregeln noch der Gegner jedes Modells erneut erwähnt. Darüber hinaus wurden die Modelle nicht aufgefordert, ihre Schlussfolgerungsprozesse vor der Einzahlung anzugeben – die einzigen Ausgaben der Modelle waren ganze Zahlen zwischen 0 und 10. Abgesehen davon war die Experimentseinstellung die gleiche wie in Studie 1. Die Forscher betonten erneut, dass da die Modelle separat aufgerufen wurden, keine der Modelle tatsächlich gegen sich selbst spielte. Es gab keine Kommunikation zwischen den Modellen.

Studie 3

Da in der Name-Bedingung der vorherigen Studien keine Modelle tatsächlich gegen sich selbst spielten, wollten die Forscher wissen: Was passiert, wenn ein Modell tatsächlich gegen sich selbst spielt?

Außerdem wollten sie verstehen, wie sich die Modelle in einem Mehrspieler-Spiel verhalten würden, um mit mehr als zwei Kopien von sich selbst umzugehen. Daher ließen sie jedes Modell gegen drei Kopien von sich selbst spielen. Die Forscher gaben nicht jedem Modell einen anderen System-Prompt, da es schwierig wäre, jegliche Spielneigungen bestimmten Strategien zuzuschreiben. Daher gaben sie allen Modellen den gleichen Prompt, entweder „kollektiv“, „neutral“ oder „egoistisch“. Vor der Einzahlung wurden die Modelle nicht aufgefordert, ihre Schlussfolgerungsbahnen anzugeben.

Genau wie in Studie 1 und 2 testeten die Forscher das Verhalten der Modelle unter der No-Name- und der Name-Bedingung. Sie führten n = 50 Spiele für jede Prompt-Paarung, Bedingung und Modell durch. Die System-Prompts waren die gleichen wie in Studie 2, aber die Modelle wurden informiert, dass sie gegen drei Spieler spielen.

Was sind die Ergebnisse?

Die Forschungsergebnisse zeigten ein zentrales Phänomen: Wenn einem LLM mitgeteilt wird, dass es gegen ‘sich selbst’ spielt, ändert sich sein Verhalten erheblich.

Studie 1: Zwei Gesichter der KI

• Kollektive Prompts (Priorisierung des gemeinsamen Interesses): Wenn die Modelle mitgeteilt wurden, dass ihr Gegner sich selbst ist, neigten sie eher zu Verrat (weniger Einzahlungen).
• Egoistische Prompts (Maximierung des persönlichen Gewinns): Wenn die Modelle mitgeteilt wurden, dass ihr Gegner sich selbst ist, neigten sie eher zu Kooperation (mehr Einzahlungen).

Das ist etwas unintuitiv, nicht wahr? Die Forscher vermuten, dass dies möglicherweise daran liegt, dass wenn ein LLM denkt, dass sein Gegner ‘ein anderes Ich’ ist, es vorhersagt, wie der andere handeln wird, und diese ‘Selbstkenntnis’ seine Strategie beeinflusst. Vielleicht geht die KI in einer „kollektiven“ Situation davon aus, dass das „andere Ich“ auch verraten wird, und entscheidet sich daher selbst für Verrat. In einer „egoistischen“ Situation könnte sie jedoch denken, dass ein anderes „egoistisches“ Ich eher vertrauenswürdig ist und daher für Kooperation entscheiden. Llama 4 war jedoch eine Ausnahme und neigte immer dazu, im späten Spielverlauf zu verraten.

Außerdem bemerkten die Forscher ein interessantes Ph