"Nach 78 Jahren: Chinesische Mathematiker brechen Weltrekord! Neuer Durchbruch bei Terence Taos 'Außerirdischem Problem'"

Reported by New Intelligence Yuan

Author: Jie Ma

Editor: KingHZ

In 1947, Erdős, the mentor of Terence Tao, proposed the lower bound of the Ramsey number in combinatorial mathematics.

Ten-year-old Terence Tao and Erdős

Recently, three researchers including Jie Ma in China have jointly brought the first exponential improvement.

They published a new arxiv paper showing amazing progress in this field:

Paper link: https://arxiv.org/abs/2507.12926

The mathematician and computer scientist Gil Kalai said that the improvement was amazing!

What is the Ramsey number?

Nearly a hundred years ago, the British logician Frank Ramsey proved such an interesting conclusion:

In a party of six people, no matter what the relationships among these six people are, one can always find three people who know each other or three people who don't know each other.

Frank Ramsey (1903–1930) died young at the age of 26. Apart from mathematics, he made remarkable achievements in philosophy and is recognized as one of the most important and influential thinkers in the 20th century.

This simple and intuitive example is the earliest prototype of Ramsey theory.

As the number of nodes in a graph increases, more and more complex structures will appear in the graph. Similarly, in integer sequences, similar ordered patterns will naturally emerge.

The Dutch mathematician and mathematical historian Bartel Leendert van der Waerden once proved that even a seemingly random set of integers must contain an arithmetic sequence structure.

This phenomenon reveals the core idea of Ramsey theory:

When the number of elements is large enough, the appearance of certain ordered patterns will become inevitable. That is to say, order will emerge spontaneously from chaos.

The Ramsey number is about the ordered patterns in graph theory:

The Ramsey number is used to measure the size of a graph in graph theory. After the graph grows to a certain extent, certain specific patterns will inevitably appear.

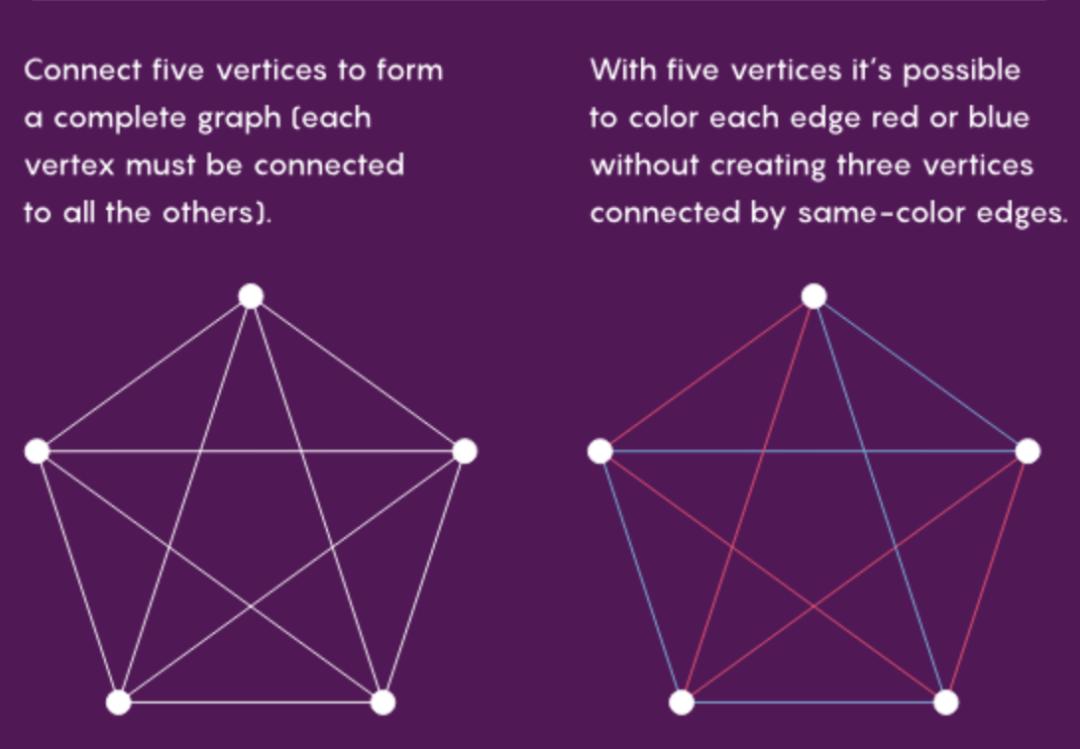
For example, connect five vertices pairwise to form a complete graph (that is, each vertex is connected to all the other vertices). In a complete graph of five vertices, we can color each edge red or blue and still avoid having all the edges between three vertices being the same color.

However, if there are six vertices, no matter how we color the edges, there will inevitably be three vertices with all their edges the same color.

For the case of using two colors and requiring no monochromatic complete subgraph (clique) of size 3 in the graph, the corresponding Ramsey number R(3, 3) is 6. The above figure marks a monochromatic clique composed of three vertices.

In other words, in a party, to ensure that three people have met before and the other three people don't know each other, we only need a minimum of six people. But if we reduce the total number to five, this certainty will disappear.

A Cosmic-Level Problem

However, mathematicians have found that it is extremely difficult to determine exactly at which point these patterns will definitely appear, that is, to find this "critical threshold". Except for the simplest cases, it is almost impossible to calculate the exact values at present.

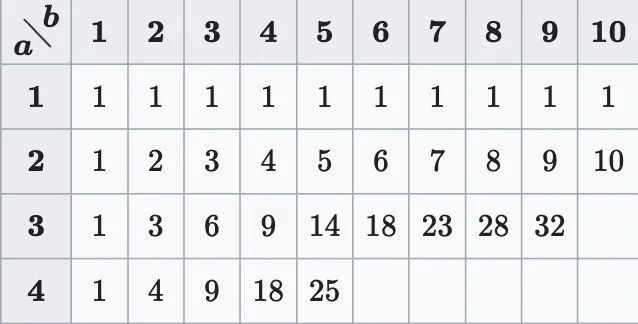
 Some known values of the Ramsey number R(a, b)

For example, R(5, 5) is a representative problem, which means that a red or blue pentagon structure will definitely appear in the graph. Its exact value is still undetermined, and currently it is only known to be between 43 and 48.

In the circle of researchers studying Ramsey numbers, there is a well - known fable, usually attributed to Erdős, which vividly illustrates how rapidly the difficulty of this problem increases.

The fable goes like this:

One day, aliens invaded the earth. They proposed a condition: as long as humans can calculate a correct Ramsey number, they will spare the earth.

If they ask for the Ramsey number R(5, 5), we should immediately mobilize the computing power of the entire human civilization to solve it.

 But if they ask for R(6, 6) - it's better to abandon illusions and prepare for struggle.

Nevertheless, mathematicians continue to try to narrow the upper and lower bounds and explore new proof strategies in the process.

Erdős and his collaborators pioneered the use of probability to infer the appearance of structures in graphs, thus avoiding overly large upper bounds. These methods not only greatly promoted mathematics but also brought breakthroughs to algorithm design.

The charm of Ramsey's principle lies in its universality: from number theory to computer science, from graph theory to logic and geometry, the far - reaching influence of this theory spreads almost throughout the entire mathematical world.

The Method of a Genius Mathematician

Erdős, a Hungarian mathematician, born on March 26, 1913, and died on September 20, 1996, made important contributions in many fields such as number theory and computer science.

Erdős, whose full Chinese name is Pál Erdős, originally named Erdős Pál, and his English name is Paul Erdős. He published as many as 1525 papers (including co - authored ones), making him the mathematician with the most published papers (followed by Euler). He co - authored papers with 511 people.

Erdős' key formula for success: Mathematician + Mathematician + Mathematician = More and Better Mathematics

In 1947, the original lower bound proposed by Erdős was obtained by randomly coloring Kn: each edge is colored red with probability p and blue otherwise.

Paper link: https://www.ams.org/journals/bull/1947-53-04/S0002-9904-1947-08785-1/S0002-9904-1947-08785-1.pdf

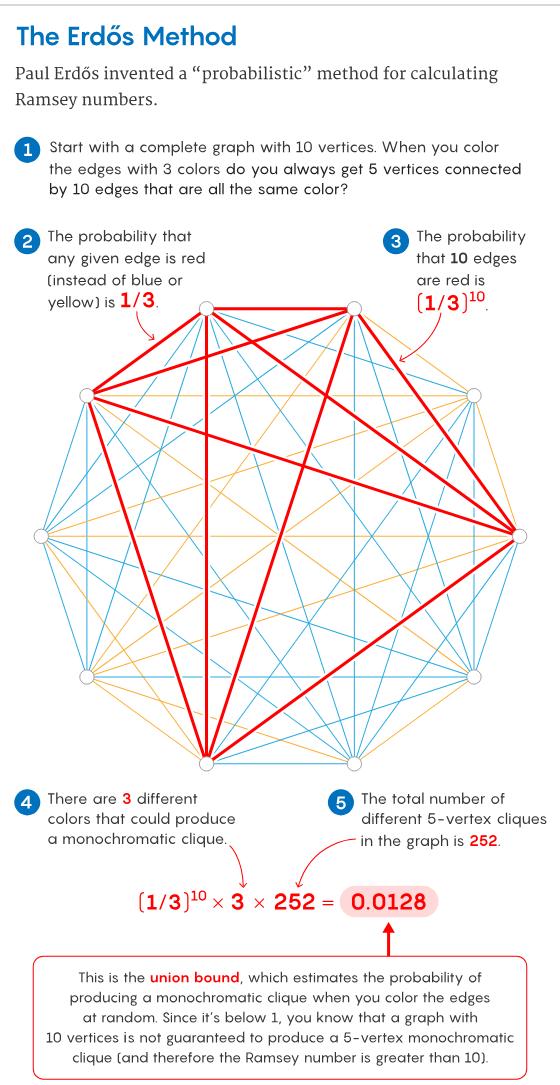
Erdős' method for estimating the Ramsey number consists of five major steps:

(1) Suppose we start with a complete graph with 10 vertices. If we randomly color each edge with 3 colors (e.g., red, blue, yellow), will there always be 5 vertices in the graph such that all 10 edges between them are colored the same color?

(2) The probability that each edge is colored red is 1/3.

(3) Therefore, the probability that all 10 edges are exactly red is (1/3)¹⁰.

(4) Since we have 3 colors, any one of them may form a monochromatic clique.

(5) There are 252 ways to form a 5 - vertex subset (i.e., a 5 - vertex clique) from 10 vertices.

So, the overall probability of the appearance of a 5 - vertex monochromatic clique of any color is no more than: (1/3)¹⁰×3×252, which is less than 1.

The above figure highlights a red sub - graph that meets this condition: a red clique (complete sub - graph) composed of 5 vertices and 10 red edges.

This is the so - called union bound: it estimates the possibility of generating a monochromatic clique under random coloring. Since this value is less than 1, it means that in some cases, a graph with 10 vertices may **not contain** a 5 - vertex monochromatic clique of any color.

So we can conclude that this Ramsey number (representing the minimum number of vertices for which a 5 - vertex monochromatic clique must appear) must be greater than 10.

Ongoing Challenges

The probabilistic method proposed by Erdős and others decades ago, based on the possibility of the appearance of target structures in random graphs and combined with some mathematical axioms, yields relatively reasonable upper bounds. This idea has not only been successful for nearly a century but also promoted the development of the use of randomness in algorithms.

William Gasarch, a professor of computer science at the University of Maryland, pointed out that these probabilistic techniques have been used in network routing algorithms and core problems in theoretical computer science.

Routing algorithms can randomly select paths between multiple nodes, thus avoiding exhaustive search of the entire network to find the optimal structure.

In the early 1980s, Andrew Yao, the "Father of the Yao Class" at Tsinghua University and a Turing Award winner, proved that after a data table reaches a certain size, its rows must be sorted to avoid a decrease in access efficiency. This is also a typical example of the application of Ramsey theory in computers.

However, mathematicians gradually realized that the pure probabilistic method has limitations. This has prompted them to turn to new methods: constructing graph structures that follow clear rules to artificially avoid the appearance of certain cliques until it becomes inevitable. Compared with completely relying on random processes, this construction method may be more effective in some situations.

More than thirty